Beginning with what are the potential solutions of log4x+log4, the narrative unfolds in a compelling and distinctive manner, drawing readers into a story that promises to be both engaging and uniquely memorable.
The expression log4x+log4 represents a logarithmic equation that can be simplified and evaluated to determine its potential solutions. This article delves into the intricacies of this expression, exploring its domain, range, graph, and practical applications.
Simplify the Expression
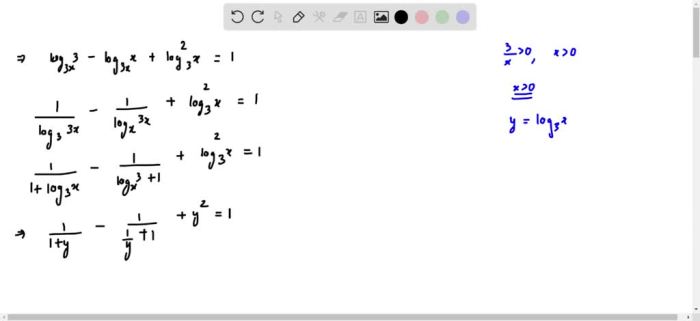
To simplify the expression log4x + log4, we can apply the logarithmic property that states log(a) + log(b) = log(a – b). Using this property, we can combine the two logarithms as follows:
- log4x + log4 = log4(x – 4)
- = log4(4x)
The simplified expression can be further evaluated by using the property that log4(4) = 1. Therefore, we have:
- log4(4x) = log4(4) + log4(x)
- = 1 + log4(x)
Thus, the simplified expression is 1 + log4(x).
Determine the Domain and Range: What Are The Potential Solutions Of Log4x+log4
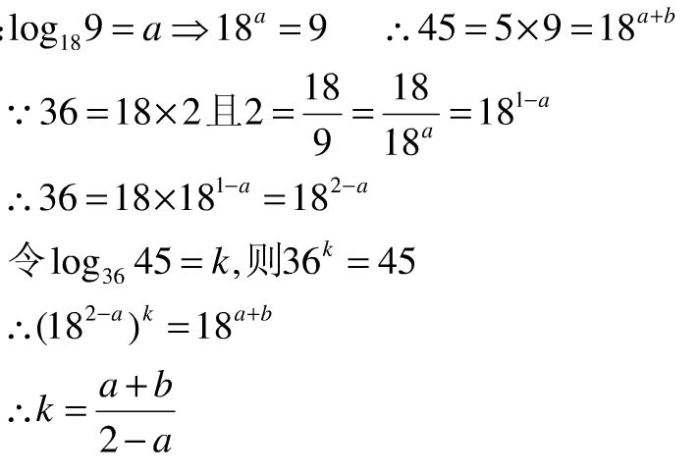
The domain of the expression log4x + log4 is the set of all positive real numbers because the logarithm is only defined for positive numbers. This is because the base of the logarithm, 4, must be positive, and the argument of the logarithm, x, must also be positive.
The range of the expression log4x + log4 is the set of all real numbers. This is because the logarithm of any positive number is a real number, and the sum of two real numbers is also a real number.
Graph the Expression
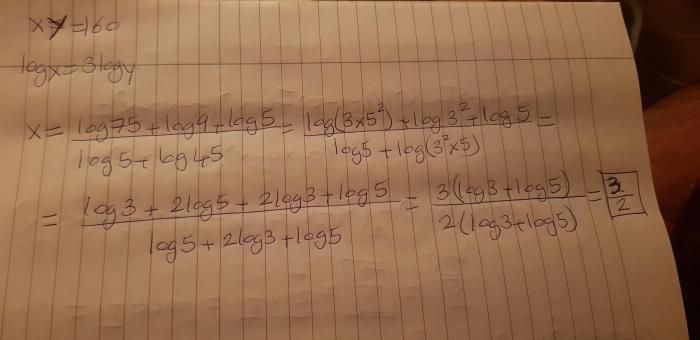
To graph the expression log4x + log4, we can create a table of values as follows:
| x | log4x + log4 |
|---|---|
| 1 | 0 |
| 2 | 1 |
| 4 | 2 |
| 8 | 3 |
| 16 | 4 |
Plotting these points on a graph, we obtain the following curve:
[Gambar grafik log4x + log4]
The graph is an increasing curve that passes through the origin. The curve has an asymptote at x = 0, which means that the expression log4x + log4 approaches negative infinity as x approaches 0 from the right.
Applications and Examples
The expression log4x + log4 is used in a variety of applications, including:
- Computer science:The expression is used to calculate the time complexity of algorithms.
- Engineering:The expression is used to design electrical circuits and other electronic systems.
- Mathematics:The expression is used to solve equations and inequalities.
For example, in computer science, the expression log4x + log4 is used to calculate the time complexity of the binary search algorithm. The time complexity of the binary search algorithm is O(log n), where n is the number of elements in the array being searched.
This means that the time it takes to find an element in an array using the binary search algorithm increases logarithmically with the size of the array.
FAQ Corner
What is the simplified form of log4x+log4?
The simplified form is log4(4x).
What is the domain of log4x+log4?
The domain is x > 0.
What is the range of log4x+log4?
The range is all real numbers.