Partitioning line segments worksheet answers are the essential elements that unlock the secrets of line segment manipulation, providing a structured approach to dividing lines into smaller parts with precision. This guide delves into the intricacies of partitioning line segments, empowering you with the knowledge and skills to tackle a wide range of mathematical and practical challenges.
Partitioning line segments is a fundamental concept in geometry, engineering, and design, with applications extending far beyond the classroom. By understanding the techniques and applications of partitioning, you gain the ability to solve complex problems, create aesthetically pleasing designs, and develop innovative solutions.
Partitioning Line Segments: Partitioning Line Segments Worksheet Answers
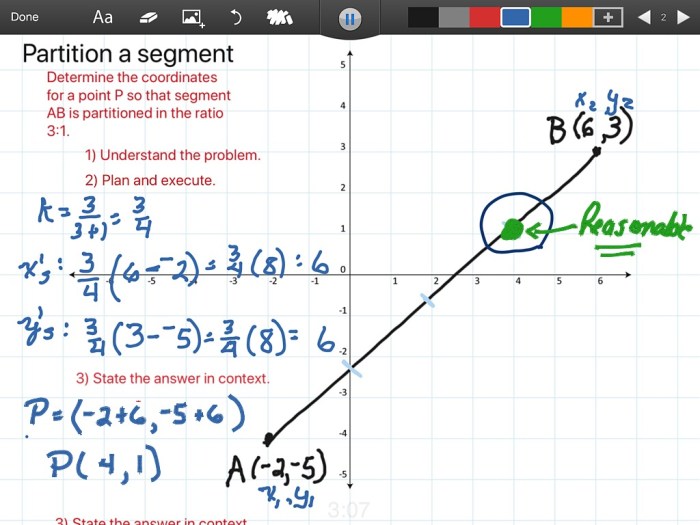
Partitioning line segments is a fundamental technique used in various fields to divide a line segment into smaller, proportional parts. This technique finds applications in mathematics, engineering, design, and more. By understanding the principles and methods of partitioning line segments, individuals can effectively solve problems and create designs.
Examples of Partitioning Line Segments, Partitioning line segments worksheet answers
- In architecture, partitioning line segments is used to determine the placement of windows, doors, and other structural elements.
- In engineering, it is used to calculate the distribution of forces and stresses on a structure.
- In design, it is used to create aesthetically pleasing and balanced compositions.
Methods for Partitioning Line Segments
There are several methods for partitioning line segments, each with its advantages and disadvantages:
| Method | Description | Advantages | Disadvantages |
|---|---|---|---|
| Midpoint Method | Divides a line segment into two equal parts. | Simple and easy to apply. | Not suitable for all applications. |
| Golden Ratio Method | Divides a line segment into two parts with a ratio of 1:1.618. | Aesthetically pleasing and often used in design. | More complex to calculate than the midpoint method. |
| Nth Part Method | Divides a line segment into n equal parts. | Versatile and applicable to various situations. | Can be tedious to calculate for large values of n. |
Applications of Partitioning Line Segments
Partitioning line segments has numerous applications across various disciplines:
- In mathematics, it is used to solve geometric problems, such as finding the area of a triangle or the volume of a pyramid.
- In engineering, it is used to design structures that are both strong and efficient.
- In design, it is used to create visually appealing and balanced compositions in art, architecture, and product design.
Advanced Concepts in Partitioning Line Segments
Advanced concepts in partitioning line segments include:
- Proportional Partitioning: Dividing a line segment into parts with specific ratios, such as the golden ratio.
- Geometric Constructions: Using geometric tools to construct line segments with specific proportions.
Popular Questions
What are the benefits of using a partitioning line segments worksheet?
Partitioning line segments worksheets provide a structured and step-by-step approach to dividing lines into smaller parts, enhancing understanding and accuracy.
How can I apply partitioning line segments in real-world scenarios?
Partitioning line segments has applications in various fields, including architecture, engineering, and design. For example, it is used to determine optimal placement of supports in structures or to create aesthetically pleasing designs.
What are the different methods for partitioning line segments?
There are several methods for partitioning line segments, including the midpoint method, the golden ratio method, and the nth part method. Each method has its advantages and disadvantages, depending on the specific application.

